Toon Shader

Toon shading (often called cel shading) is a rendering style designed to make 3D surfaces emulate 2D, flat surfaces. This style entered the mainstream with games like Jet Set Radio and The Wind Waker.

This tutorial will describe step-by-step how to write a toon shader in Unity. The shader will receive light from a single directional source, and have specular reflections and rim lighting. We will use the art style of The Legend of Zelda: Breath of the Wild as our reference, although we will not implement some of the more complex rendering techniques used in the game.

Prerequisites

To complete this tutorial, you will need a working knowledge of Unity engine, and a basic understanding of shader syntax and functionality.

Download starter project .zip

Getting started

Download the starter project provided above and open it in the Unity editor. Open the Main scene, and open the Toon shader in your preferred code editor.

This file contains a simple shader that outputs a sampled texture, tinted by a color (with the default color set to cornflower blue). We will build off this file to create our toon shader.

1. Directional lighting

When writing shaders in Unity that interact with lighting it is common to use Surface Shaders. Surface shaders use code generation to automate the object's interaction with lights and global illumination. However, as our shader will only interact with a single directional light, it will not be necessary to use surface shaders.

We will set up our shader to receive lighting data. Add the following code at the top of the Pass, just after its opening curly brace.

Tags
{
	"LightMode" = "ForwardBase"
	"PassFlags" = "OnlyDirectional"
}

The first line requests some lighting data to be passed into our shader, while the second line further requests to restrict this data to only the main directional light. You can read more about Pass tags here.

To calculate our lighting, we will use a common shading model called Blinn-Phong, and apply some additional filters to give it a toon look. The first step is to calculate the amount of light received by the surface from the main directional light. The amount of light is proportional to the direction, or normal of the surface with respect to the light direction.

We'll need access to the object's normal data within our shader. Add the following code.

// Inside the appdata struct.
float3 normal : NORMAL;

…

// Inside the v2f struct.
float3 worldNormal : NORMAL;

The normals in appdata are populated automatically, while values in v2f must be manually populated in the vertex shader. As well, we want to transform the normal from object space to world space, as the light's direction is provided in world space. Add the following line to the vertex shader.

o.worldNormal = UnityObjectToWorldNormal(v.normal);

With the world normal now available in the fragment shader, we can compare it to the light's direction using the Dot Product.

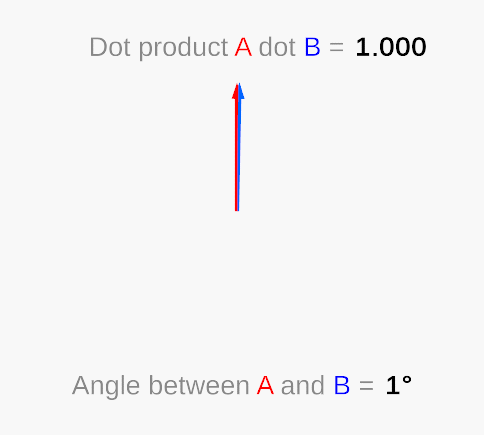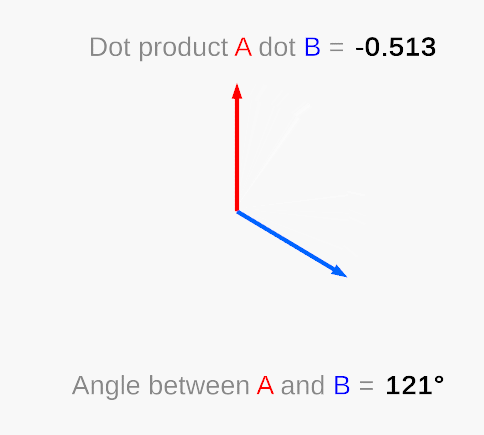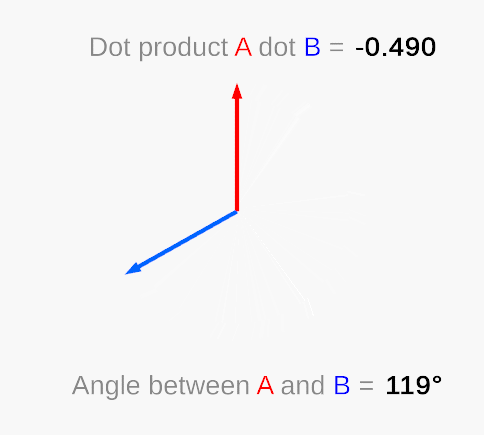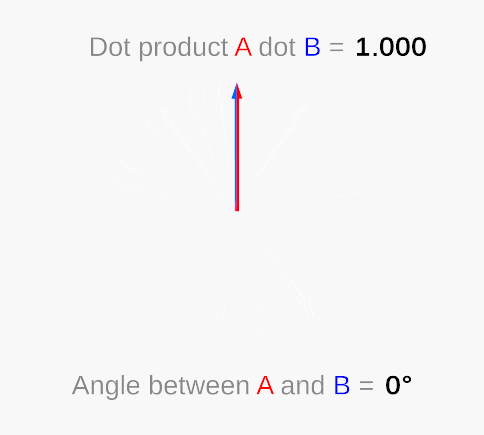
The dot product takes in two vectors (of any length) and returns a single number. When the vectors are parallel in the same direction and are unit vectors (vectors of length 1), this number is 1. When they are perpendicular, it returns 0. As you move a vector away from parallel—towards perpendicular—the dot product result will move from 1 to 0 non-linearly. Note that when the angle between the vectors is greater than 90, the dot product will be negative.

Add the following to the fragment shader. Note that existing code that is modified will be highlighted in yellow. New code is not highlighted.

// At the top of the fragment shader.
float3 normal = normalize(i.worldNormal);
float NdotL = dot(_WorldSpaceLightPos0, normal);

…

// Modify the existing return line.
return _Color * sample * NdotL;

This has rendered out a realistic style of illumination. To modify it to be toon-like, we will divide the lighting into two bands: light and dark.

// Below the NdotL declaration.
float lightIntensity = NdotL > 0 ? 1 : 0;

…

return _Color * sample * lightIntensity;

2. Ambient light

This looks good, but the dark side is too dark; right now it is completely black. Also, the edge between dark and light looks a bit sharp, but we'll deal with that later. For now, we will add ambient light.

Ambient light represents light that bounces off the surfaces of objects in the area and is scattered in the atmosphere. We will model it as a light that affects all surfaces equally and is additive to the main directional light.

// Add as a new property.
[HDR]
_AmbientColor("Ambient Color", Color) = (0.4,0.4,0.4,1)

…

// Matching variable, add above the fragment shader.
float4 _AmbientColor;

…

return _Color * sample * (_AmbientColor + lightIntensity);

You'll notice that modifying the intensity or color of the Directional Light in the scene does not affect our shader. We will add some code to include this in our lighting calculations.

// Add below the existing #include "UnityCG.cginc"
#include "Lighting.cginc"

…

// Add below the lightIntensity declaration.
float4 light = lightIntensity * _LightColor0;

…

return _Color * sample * (_AmbientColor + light);

We multiply our existing lightIntensity value and store it in a float4, so that we include the light's color in our calculation. _LightColor0 is the color of the main directional light. It is a fixed4 declared in the Lighting.cginc file, so we include the file above to make use of the value.

Before going further, we'll soften the edge between light and dark to remove the jaggedness. Right now, the transition from light to dark is immediate and occurs over a single pixel. Instead, we'll smoothly blend the value from one to zero, using the smoothstep function.

smoothstep takes in three values: a lower bound, an upper bound and a value expected to be between these two bounds. smoothstep returns a value between 0 and 1 based on how far this third value is between the bounds. (If it is outside the lower or upper bound, smoothstep returns a 0 or 1, respectively).

smoothstep is not linear: as the value moves from 0 to 0.5, it accelerates, and as it moves from 0.5 to 1, it decelerates. This makes it ideal for smoothly blending values, which is how we'll use it to blend our light intensity value.

float lightIntensity = smoothstep(0, 0.01, NdotL);

Our lower and upper bounds, 0 and 0.01, are very close together—this helps maintain a relatively sharp, toony edge. When NdotL is above 0.01 or below 0 it returns one and zero like before, respectively. However, in between that range it will smoothly blend between 0 and 1.

3. Specular reflection

Specular reflection models the individual, distinct reflections made by light sources. This reflection is view dependent, in that it is affected by the angle that the surface is viewed at. We will calculate the world view direction in the vertex shader and pass it into the fragment shader. This is the direction from the current vertex towards the camera.

// Add to the v2f struct.
float3 viewDir : TEXCOORD1;

…

// Add to the vertex shader.
o.viewDir = WorldSpaceViewDir(v.vertex);

We'll now implement the specular component of Blinn-Phong. This calculation takes in two properties from the surface, a specular color that tints the reflection, and a glossiness that controls the size of the reflection.

// Add as new properties.			
[HDR]
_SpecularColor("Specular Color", Color) = (0.9,0.9,0.9,1)
_Glossiness("Glossiness", Float) = 32

…

// Matching variables.
float _Glossiness;
float4 _SpecularColor;

The strength of the specular reflection is defined in Blinn-Phong as the dot product between the normal of the surface and the half vector. The half vector is a vector between the viewing direction and the light source; we can obtain this by summing those two vectors and normalizing the result.

// Add to the fragment shader, above the line sampling _MainTex.
float3 viewDir = normalize(i.viewDir);

float3 halfVector = normalize(_WorldSpaceLightPos0 + viewDir);
float NdotH = dot(normal, halfVector);

float specularIntensity = pow(NdotH * lightIntensity, _Glossiness * _Glossiness);

…

return _Color * sample * (_AmbientColor + light + specularIntensity);

We control the size of the specular reflection using the pow function. We multiply NdotH by lightIntensity to ensure that the reflection is only drawn when the surface is lit. Note that _Glossiness is multiplied by itself to allow smaller values in the material editor to have a larger effect, and make it easier to work with the shader.

Once again we will use smoothstep to toonify the reflection, and multiply the final output by the _SpecularColor.

// Add below the specularIntensity declaration.
float specularIntensitySmooth = smoothstep(0.005, 0.01, specularIntensity);
float4 specular = specularIntensitySmooth * _SpecularColor;

…

return _Color * sample * (_AmbientColor + light + specular);

4. Rim lighting

Rim lighting is the addition of illumination to the edges of an object to simulate reflected light or backlighting. It is especially useful for toon shaders to help the object's silhouette stand out among the flat shaded surfaces.

The "rim" of an object will be defined as surfaces that are facing away from the camera. We will therefore calculate the rim by taking the dot product of the normal and the view direction, and inverting it.

// In the fragment shader, below the line declaring specular.
float4 rimDot = 1 - dot(viewDir, normal);

…

return _Color * sample * (_AmbientColor + light + specular + rimDot);

Once again, we'll toonify the effect by thresholding the value with smoothstep.

// Add as new properties.
[HDR]
_RimColor("Rim Color", Color) = (1,1,1,1)
_RimAmount("Rim Amount", Range(0, 1)) = 0.716

…

// Matching variables.
float4 _RimColor;
float _RimAmount;

…

// Add below the line declaring rimDot.
float rimIntensity = smoothstep(_RimAmount - 0.01, _RimAmount + 0.01, rimDot);
float4 rim = rimIntensity * _RimColor;

…

return _Color * sample * (_AmbientColor + light + specular + rim);

With the rim being drawn around the entire object, it tends to resemble an outline more than a lighting effect. We'll modify it to only appear on the illuminated surfaces of the object.

// Add above the existing rimIntensity declaration, replacing it.
float rimIntensity = rimDot * NdotL;
  rimIntensity = smoothstep(_RimAmount - 0.01, _RimAmount + 0.01, rimIntensity);

This is better, but it would be useful to be able to control how far the rim extends along the lit surface. We'll use the pow function to scale the rim.

// Add as a new property.
_RimThreshold("Rim Threshold", Range(0, 1)) = 0.1

…

// Matching variable.
float _RimThreshold;

…

float rimIntensity = rimDot * pow(NdotL, _RimThreshold);

5. Shadows

As a final step, we will add the ability for our shader to cast and receive shadows. Shadow casting is very simple. Add the following line of code below the entire Pass (outside the curly braces).

// Insert just after the closing curly brace of the existing Pass.
UsePass "Legacy Shaders/VertexLit/SHADOWCASTER"

UsePass grabs a pass from a different shader and inserts it into our shader. In this case, we are adding a pass that is used by Unity during the shadow casting step of the rendering process.

In order to receive shadows, we will need to know in the fragment shader whether a surface is in a shadow or not, and factor that in to our illumination calculation. To sample the shadow map cast by a light, we'll need to transfer texture coordinates from the vertex shader to the fragment shader.

// As a new include, below the existing ones.
#include "AutoLight.cginc"

…

// Add to the v2f struct.
SHADOW_COORDS(2)

…

// Add to the vertex shader.
TRANSFER_SHADOW(o)

We include Autolight.cginc, a file that contains several macros we will use to sample shadows. SHADOW_COORDS(2) generates a 4-dimensional value with varying precision (depending on the target platform) and assigns it to the TEXCOORD semantic at the provided index (in our case, 2).

TRANSFER_SHADOW transforms the input vertex's space to the shadow map's space, and then stores it in the SHADOW_COORD we declared.

Before we can sample the shadow map, however, we need to ensure our shader is set up to handle two different lighting cases: when the main directional light does and does not cast shadows. Unity will help us handle these two configurations by compiled multiple variants of this shader for each use case. You can read more about shader variants here. We will use a built-in shortcut to compile our variants. Add the following line of code just below the #pragma fragment frag line.

#pragma multi_compile_fwdbase

This shortcut instructs Unity to compile all variants necessary for forward base rendering. We can now sample the value in the shadow map, and apply it to our lighting calculation.

// In the fragment shader, above the existing lightIntensity declaration.
float shadow = SHADOW_ATTENUATION(i);

float lightIntensity = smoothstep(0, 0.01, NdotL * shadow);

SHADOW_ATTENUATION is a macro that returns a value between 0 and 1, where 0 indicates no shadow and 1 is fully shadowed. We multiply NdotL by this value, as it is the variable that stores how much light we received from the main directional light.

Conclusion

Toon shaders come in a wide variety of graphical styles, but achieving the effect usually centers around taking a standard lighting setup (as we did with Blinn-Phong) and applying a step function to it. In fact, when normals and lighting data is available it can be done as a post process effect. An example of this can be found in this tutorial for Unreal Engine 4.

View source GitHub repository

Leave me a message

You can contact me about this article at Copied to clipboardroystanhonks@gmail.com 📋 roystanhonks@gmail.com 📧 . Sometimes I receive a lot of messages, but I'll try and get back to you as soon as I can!